LQR
(Linear Quadratic Regulator) Nedir?

Lineer kuadratik regulator(LQR), mühendislik uygulamalarında kullanılan optimal kontrol yöntemlerinden biridir. PID kontrol yönteminden farklı olarak MIMO (Çok Girişli-Çok Çıkışlı) sistemler için kullanılabilen bu kontrol yöntemini inceleyeceğiz. Detaylar yazımızda.

A- A+

21.10.2021 tarihli yazı 7454 kez okunmuştur.

Klasik optimal kontrol problemlerinden biri olan LQR, x ̇= Ax ̇+ Bu şeklinde tanımlı doğrusal, zamandan bağımsız dinamik bir sistemimiz olsun. Bu sebepten K kazanç matrisini belirlemek daha doğrusu K kazanç matrisini belirleyen uygun Q ve R ağırlık matrislerini hesaplamak kontrol açısından son derece önem arz etmektedir. Literatürde özellikle K kazanç matrisinin nümerik optimizasyon yöntemleriyle belirlendiği bir çok çalışma bulunmaktadır.

►İlginizi Çekebilir: PID DENETLEYİCİLER

Standart LQR problemlerinde performans (y ̇=Cx ̇+Du) gibi bir çıktı cinsinden de tanımlanabilir. Bu durumda performans kriteri çıktının enerjisi olmaktadır.

Problemin çözümü cebirsel bir riccati denkleminin çözümüne eşdeğerdir. Sonuçta bulunan optimal regulator, statik durum geri beslemesinden ibarettir.

Optimum kontrol teorisi, dinamik bir sistemin minimum maliyetle çalıştırılmasıyla ilgilidir. Sistem dinamiğinin bir dizi lineer diferansiyel denklemle tanımlandığı ve maliyetin ikinci dereceden bir fonksiyonla tanımlandığı duruma LQ problemi denir. Teorideki ana sonuçlardan biri, çözümün denklemleri aşağıda verilen bir geri besleme denetleyicisi olan lineer-quadratik regulator (LQR) tarafından sağlanmasıdır. LQR, LQG (doğrusal-kuadratik-Gauss) probleminin çözümünün önemli bir parçasıdır . LQR probleminin kendisi gibi, LQG problemi de kontrol teorisindeki en temel problemlerden biridir.

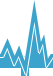
Bir makineyi veya işlemi yöneten bir denetleyicinin ayarları, bir insan tarafından sağlanan ağırlıklandırma faktörleriyle bir maliyet fonksiyonunu en aza indiren matematiksel bir algoritma kullanılarak bulunur . Maliyet fonksiyonu genellikle yükseklik veya proses sıcaklığı gibi temel ölçümlerin istenen değerlerden sapmalarının toplamı olarak tanımlanabilir. Algoritma böylece istenmeyen sapmaları en aza indiren kontrolör ayarlarını bulur. Kontrol eyleminin büyüklüğü de maliyet fonksiyonuna dahil edilir.Aşağıdaki çıktıda LQR kontrolcüsünün geleneksel PI kontrolsücüsüne göre avantajı acıkça görülmektedir.

LQR algoritması, kontrolörü optimize etmek için kontrol mühendisi tarafından yapılan iş miktarını azaltır. Ancak mühendisin yine de maliyet fonksiyonu parametrelerini belirlemesi ve sonuçları belirtilen tasarım hedefleriyle karşılaştırması gerekmektedir. Bu genellikle, kontrolcünün yapısının, mühendisin simülasyon yoluyla üretilen "optimal" kontrolcüleri incelediği ve ardından tasarım hedefleriyle daha tutarlı bir kontrolcü üretmek için parametreleri yeniden ayarladığı anlamına gelmektedir.

LQR algoritması, uygun bir geri bildirim denetleyicisi bulmanın otomatik bir yoludur . Bu nedenle, kontrol mühendislerinin, kontrolcü parametreleri ile kontrolcü davranışı arasında daha net bir ilişkinin olduğu görülmektedir. Doğru ağırlık faktörlerini bulmadaki zorluk, LQR tabanlı kontrolcü sentezinin uygulanmasını sınırlayan etmenlerden birkaçıdır.

LQR Teorisi ve Nümerik Analizi

Yukarıda verilen eşitilikler sayesinde çok girişli ve çok çıkışlı bir sistem tasarımının kotrolü LQR kontrolcüsü kullanılarak en az maliyet ile hesaplanabilmektedir.

Kaynak:

►Matematiksel Kontrol Teorisi: Deterministik Sonlu Boyutlu Sistemler (Kitap)
►Lineer Optimal Kontrol Sistemleri, Dinamik Ekonomik Sistemlerin Analizi ve Kontrolü (Kitap)
►LQR Algoritmasi ile Kuadrokopter Kontrolü Yüksek Lisans Tezi