Milyon Dolarlık 7 Soru
Belkibirçoğunuz duymuşsunuzdur. Matematikte efsane olmuş 7 tane problem ve her biriiçin konulmuş bir milyon dolarlık ödül vardır. Soruların zorluğu ve yüzyıldırçözülememiş olmasının yanında sanırım her biri için konulan ödülün de busorularının popülaritesi arttırdığını söyleyebiliriz. Şimdi bu yazıda bu sorularınhangileri olduğunu ve çözümlerin getirdiği incelemeleri bulacaksınız.
7 Soru – 7 Ödül
1-Goldbach Kestirimi
2-Asal Sayılardan Karışık
3-Mükemmel Sayı Sorusu
4-Palindromik Sayılar
5-Collatz Problemi
6-Riemann Hipotezi
7-Binyılın Problemleri
Goldbach Kestirimi
1742'de Goldbach, Euler'e yazdığı bir mektupta "2'den büyük her çift sayı, iki asal sayının toplamı şeklinde ifade edilebilir" önermesinin, ya doğru olduğunu ispatlamasını ya da bunu sağlamayan bir örnek göstererek yanlış olduğunu ispatlamasını istedi. Bu hipotezle asal sayılar konusuna yeni bir heyecan gelmiştir. Ancak şimdiye kadar kimse ne bu sorunun doğruluğunu ne de yanlışlığını ispat edebilmiştir.
Ayrıca, 2'den başlayarak her çift sayıya 3 sayısı (ki bu bir asal sayı) ekleyerek tek sayılar kümesi elde edilebildiğine göre (örneğin:5=2+3; 7=4+3; 9=6+3...) her çift sayı 2 asal sayının toplamı ise her tek sayı da üç asal sayının toplamıdır denilebilir. Bu ifade de zayıf (ya da tek) Goldbach kestirimi olarak bilinir. Ve bunun da henüz bir yanıtı yoktur.
Asal Sayılardan Karışık
Asal sayıları matematiğin en ilginç konularından biridir. Hala bu konuya ilişkin bir çok soru gün ışığına çıkarılamadı. Ortaya atılan ancak ispatlanamamış bir çok problem bulunur.
* n2 ve (n + 1)2 arasında daima bir asal var mıdır?
* İkiz Asallar: İkiz asallar yani aralarındaki fark 2 olan asallar sonsuz tane midir?
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43). ..???
* Bugün hala sonsuz tane elemanı olduğu tam olarak ispatlanmayan (ama öyle olduğu tahmin edilen) bir diğer küme de farkı 2n olan asal çiftlerinin oluşturduğu kümelerin hepsinin sonsuz tane eleman içerdiği sanısı. Bu kestirimi ortaya atarak problemi genel bir boyuta taşıyansa Alphonse de Polignac (1849)’tır. Örneğin Kuzen asallar olarak bilinen aralarındaki fark 4 olan asal sayıların oluşturduğu küme sonsuz eleman içerir mi?
* (n2 +1) formunda yazılabilen sonsuz tane asal var mıdır?
* Fermat Asalları: 17. yüzyılda amatör matematikçi ünvanı ile bilinen Fermat asal sayılar konusuna oldukça önemli katkılarda bulundu. Araştırmaları arasında doğru olduğu tahmin edilen ama ispatlanamayan sorular da vardır. Örneğin 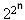 + 1 biçimindeki sayıların her n doğal sayısı için bir asal verdiğini iddia edilmektedir. Bu biçimdeki sayılara Fermat sayıları, asal olanlara da Fermat asalları denir. Gerçekten de 5'e kadar tüm doğal sayılar için asal değer veren ifadenin yanlış olduğu ancak 100 yıldan fazla zaman sonra anlaşılabildi. n=5 için 232 + 1 = 4294967297 sayısının 641 ile bölündüğünün farkına varansa Euler oldu. Bugün ispatı yapılması beklenen önermelerden bir diğeriyse "Fermat asalları sonlu tanedir" kestirimi. Bu ifadenin en güçlü gerekçesiyse şimdiye kadar sadece 5 tane Fermat asalının bulunmasıdır
+ 1 biçimindeki sayıların her n doğal sayısı için bir asal verdiğini iddia edilmektedir. Bu biçimdeki sayılara Fermat sayıları, asal olanlara da Fermat asalları denir. Gerçekten de 5'e kadar tüm doğal sayılar için asal değer veren ifadenin yanlış olduğu ancak 100 yıldan fazla zaman sonra anlaşılabildi. n=5 için 232 + 1 = 4294967297 sayısının 641 ile bölündüğünün farkına varansa Euler oldu. Bugün ispatı yapılması beklenen önermelerden bir diğeriyse "Fermat asalları sonlu tanedir" kestirimi. Bu ifadenin en güçlü gerekçesiyse şimdiye kadar sadece 5 tane Fermat asalının bulunmasıdır

*Mersenne Asalları: Fermat'ın sıkça fikir alışverişinde bulunduğu çağdaşı Mersenne 2n - 1 şeklindeki sayılar üzerinde çalışıyordu. Mersenne sayıları (Mn) adı verilen bu sayıların başlangıçta n asal olduğunda asal değer verdiği düşünüldü. Gerçekten de n=11'e kadar doğru çalışan fikir 11'de asal olmayan bir değer alınca bu düşüncenin de yanlış olduğu anlaşılabildi ama 2n - 1'in asal olması için n'nin asal olması gerektiği şartı doğrudur. Yine de matematikçiler bu sayıların peşini bırakmadı. Sonsuz tane olup olmadıkları hala merak edilen Mersenne sayılarından Aralık 2005 itibariyle 43.sü bulundu.
Mükemmel Sayı Sorusu
Mükemmel sayı kendisi haricindeki tüm çarpanlarının toplamı kendisini veren sayıdır. Örneğin 6 bir mükemmel sayıdır çünkü kendisi haricindeki çarpanları yani 1, 2 ve 3 toplanınca kendisini verir: 1 + 2 + 3 = 6. Diğer örneklerse 28, 496, 8128 şeklinde gidiyor. Şimdiye kadar hiç tek mükemmel bir sayıya rastlanmamış. Merak edilen böyle bir sayının var olup olmadığı. Eğer vardır diyorsanız bunu bulmak ve matematik tarihine geçmek tamamen size kalmıştır.
Palindromik Sayılar
Kapak, kütük, sus, yay, kepek kelimeleri ilginç bir ortak özellik ile dikkat çekiyor: düzden ve tersten okunduğunda aynı. Benzer bir yapıya sahip olan palindromik sayılar da düzden ve tersten okunduğunda aynı olan sayılardır:
1991, 10001, 12621, 79388397, 82954345928.
Bu alandaki açık soru ise şöyle:
Hem asal hem de palindromik olan sonsuz tane asal sayı bulunabilir mi?
Collatz Problemi
Önce bir pozitif tamsayı seçin. Bu sayıya yapılacak işlem şu:
Sayı tekse 3 katını alıp 1 ekleyin. Sayı çiftse 2'ye bölün.
Aynı işleme çıkan sayıya uygulayın. En sonunda elde edeceğiniz sayı1'dir.
Örneğin 8 sayısını ele alalım:
8-(2'ye böl)-4-(2'ye böl)-2-(2'ye böl)-1
5-(3 katını al 1 ekle)-16-8-4-2-1
Seçtiğiniz sayıya dikkat edin. Örnek olarak 27 sayısını seçtiyseniz 1 sayısını bulmanız için 112 basamak ilerlemeniz gerektiriyor. Tabi kaç basamak alacağı sayının büyük veya küçük olmasıyla ilgili değil. Sadece bu algoritmanın her zaman 1 cevabını verdiğini ispatlamanın peşinde koşmayın. Unutmayın ki sonunda 1 vermeyen bir sayı da var olabilir ve bu da, sorunun cevaplandığı anlamına gelir.
Riemann Hipotezi
Bilindiği gibi asal sayılar düzenli bir dağılıma sahip değiller. Alman matematikçi G.F.B. Riemann (1826 - 1866) asal sayıların dağılımlarının Riemann-Zeta adını verdiği bir fonksiyon ile çok yakından ilişkili olduğunu gözlemledi. Söz konusu olan fonksiyon şöyle:
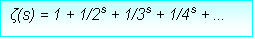
Bu fonksiyon s'nin 1 dışındaki her kompleks sayı değeri için tanımlıdır.
Riemann Hipotezine göre bu fonksiyonun,  (s) = 0 ifadesini sağlayan tüm önemsiz olmayan s değerleri, reel kısmı ½ olan düşey doğru üzerine düşer (bu doğruya kritik doğru deniyor). İlk 1 500 000 000 değer için bu doğruluk tespit edilmiş olsa da asıl istenen, söz konusu tüm değerler için doğru olduğunun ispatlanmasıdır. Bu sorunun başında da 1 milyon dolarlık ödül konulduğunu unutmayın!
(s) = 0 ifadesini sağlayan tüm önemsiz olmayan s değerleri, reel kısmı ½ olan düşey doğru üzerine düşer (bu doğruya kritik doğru deniyor). İlk 1 500 000 000 değer için bu doğruluk tespit edilmiş olsa da asıl istenen, söz konusu tüm değerler için doğru olduğunun ispatlanmasıdır. Bu sorunun başında da 1 milyon dolarlık ödül konulduğunu unutmayın!
Binyılın Problemleri: 1 milyon dolar kazanmak isteyenlere!
1 milyon dolar, yani bugün yaklaşık 1,7 milyon YTL (1,7 trilyon TL) kazanmak ister misiniz? Bunun için yapmanız gereken tek şey bu 7 sorudan birini çözmek. Defter, kitap serbest; süre sınırlaması da yok! Cevabı ilk veren siz olun da isterseniz aradan 100 yıl geçsin. Yalnız şunu unutmayın, bu sorular yıllardır peşinden onlarca, yüzlerce insanı, bilim adamını sürükleyen ve ne kadar uğraşılsa da çözülemeyen sorulardır. Ve ayrıca eğer ki doğru cevabı bulursanız yaşam standartınızı tamamen değiştirecek sorulardır. İlginç olansa başarıya ulaşan insanlar, özellikle de matematikçiler, bu paranın hayalini kurdukları için değil matematik yapmayı sevdikleri ve bu alanda başarı istedikleri için kolları sıvıyorlar. Para, bu başarının sonunda gelen bir ödülden başka bir şey değil, onlar için.
Cambridge Massachusetts 'de kurulan Clay Matematik Enstitüsü, 24 Mayıs 2000'de çözülmekte inatçı, matematiğin farklı branşlarındaki 7 problemini Milenyum Problemleri olarak adlandırdığını ve her bir problemi ilk çözen kişiye 1'er milyon dolar vereceğini ilan etti. Bu soruları anlamak, bir parça matematik temeli gerektiriyor. Bu durum matematiğin, hızla büyümesinin ve lise eğitiminin onu yakalamaya yetmemesinin bir sonucu olabilir. Soruları anlamak için üniversitede matematik okumak şart değil elbette, sadece Fermat'ın son teoremini, Goldbach ya da ikiz asallar kestirimini anlamaktan daha fazla çaba sarfetmek lazım. Eğer Riemann Hipotezi, P, NP' ye karşı Hodge Kestirimi, Yang-mills Kuramı, Poincare Kestirimi, Navier Stokes denklemleri, Birch ve Swinnerton-Dyer Kestirimi başlıklı sorulardan birinin yanıtını bulduysanız bu organizasyonu yapan Clay Matematik Enstitüsü'ne yollamadan önce uluslararası kabul gören hakemli bir dergide yayınlamanız gerekiyor. Daha ayrıntılı bilgi için www.claymath.org
*Clay Enstitüsü'nün belirlemiş olduğu bu 7 problemin 1 tanesi, Pointcaré Kestirimi 2006'da resmi olarak teorem haline geldi. Petersburg'daki Steklov Enstitüsü matematikçilerinden Grişa Perelman'ın 2002'de yayınladığı ispatın doğru olduğu resmen 2006 Dünya Matematikçiler Birliği'nin Madrid'teki kongresinde açıklandı. Diğer taraftan, Navier-Stokes Denklemleri'nin de 2006 içinde çözüldüğü duruldu. Ancak değerlendirmeler devam ediyor. Şu an için 1000 yılın problemlerinden çözüm bekleyenlerin sayısı 5 taneye düşmüş gözüküyor.
Yukarda da belirttiğim gibi sorulardan biri, Grigori Yakovlevich Perelman isimli bir rus matematikçi tarafından çözülmüştür. 2002’de çözüp yayınladıktan sonra, 2006’da kabul görmesinden sonra kendisine verilen hem 1 milyon dolarlık ödülünü hem de matematiğin Nobel’i sayılan Fields ödülünü reddetmiştir.
“Para ya da şöhretle ilgilenmiyorum. Bir hayvanat bahçesindeki hayvan gibi sergilenmek istemiyorum. Ben matematik kahramanı değilim. Hatta başarılı bile değilim. Bu yüzden herkesin bana bakmasını istemiyorum. “ sözü sanırım ödülü almamasının kendince nedenidir. 2003'te St. Petersburg'da Steklov Matematik Enstitüsü'nde araştırmacı olan Perelman, internetten Poincare Varsayımı'nı çözdüğünü söyleyen çalışmalarını yayınlamaya başladı. Perelman'ın çözümünün doğru olduğu anlaşıldı.
Çözümün, evrenin şeklinin belirlenmesine yardımcı olabileceği kaydediliyor. 2003'ten sonra Perelman işini bıraktı. Arkadaşları tamamen matematiği bıraktığını söylemişti.
Emre Berk Sevinç
-
 Dünyanın En Görkemli 10 Güneş Tarlası
Dünyanın En Görkemli 10 Güneş Tarlası
-
 Dünyanın En Büyük 10 Makinesi
Dünyanın En Büyük 10 Makinesi
-
 2020’nin En İyi 10 Kişisel Robotu
2020’nin En İyi 10 Kişisel Robotu
-
 Programlamaya Erken Yaşta Başlayan 7 Ünlü Bilgisayar Programcısı
Programlamaya Erken Yaşta Başlayan 7 Ünlü Bilgisayar Programcısı
-
 Üretimin Geleceğinde Etkili Olacak 10 Beceri
Üretimin Geleceğinde Etkili Olacak 10 Beceri
-
 Olağan Üstü Tasarıma Sahip 5 Köprü
Olağan Üstü Tasarıma Sahip 5 Köprü
-
 Dünyanın En İyi Bilim ve Teknoloji Müzeleri
Dünyanın En İyi Bilim ve Teknoloji Müzeleri
-
 En İyi 5 Tıbbi Robot
En İyi 5 Tıbbi Robot
-
 Dünyanın En Zengin 10 Mühendisi
Dünyanın En Zengin 10 Mühendisi
-
 Üretim için 6 Fabrikasyon İşlemi
Üretim için 6 Fabrikasyon İşlemi
-
 Sigma Termik Manyetik Şalterler ile Elektrik Devrelerinde Koruma
Sigma Termik Manyetik Şalterler ile Elektrik Devrelerinde Koruma
-
 Elektrik Panoları ve Üretim Teknikleri
Elektrik Panoları ve Üretim Teknikleri
-
 Teknik Servis | Megger Türkiye
Teknik Servis | Megger Türkiye
-
 Güneş Enerji Santrallerinde Yıldırımdan Korunma ve Topraklama
Güneş Enerji Santrallerinde Yıldırımdan Korunma ve Topraklama
-
 Megger Türkiye Ofisi
Megger Türkiye Ofisi
-
 STX40 Taşınabilir Kablo Arıza Tespit Sistemi | Megger
STX40 Taşınabilir Kablo Arıza Tespit Sistemi | Megger
-
 Megger digiPHONE + 2 Kablo Tespit Sistemi Nasıl Kullanılır
Megger digiPHONE + 2 Kablo Tespit Sistemi Nasıl Kullanılır
-
 Kontaktör ve Termik Röle Seçimi & Uygulamaları
Kontaktör ve Termik Röle Seçimi & Uygulamaları
-
 Yıldırımdan Korunma Sistemleri | Amper Elektrik
Yıldırımdan Korunma Sistemleri | Amper Elektrik
-
 Toprak Kaçak Akım Rölesi ve Toroid Akım Trafoları
Toprak Kaçak Akım Rölesi ve Toroid Akım Trafoları









 Baycan Karabağ
Baycan Karabağ